
Existen muchas formas de resolver estas raices primero estudiaremos como se aplican en el Metodo de Newton-Raphson
Notas sobre el uso de las Raices




Asi mismo los numeros complejos tienen todas las propiedades de los numeros reales
//////////////////////
En este metodo se tiene que despejar a la variable independiente:

donde es la funcion de busqueda que cumple el problema de convergencia.


Ejemplo:
1.- x - cosx = 0
x = cos x ..... 1
cos-1x = x .... 2

///////////////////////
El metodo de la secante
Ecuacion de Newton-Raphson:

la definicion dederivada si escogieramos 2 numeros n+1 y Xn muy cercanos

EN donde Xo es la "peor aproximacion" y Xi es la "aproximacion mejorada"
Xo es la aproximacion tal que:
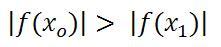
////////
Metodo de Newton-Raphson
martes 24 de marzo de 2009 Publicado por . en 19:21

la recta tangente k se observa que:
dy/dx = m= cte
dy = mdx= F’(X0)(X- X0)
y – y0 = F’(X0)(X- X0)
F(x)- F(X0) = F’(X0)(X- X0)
- F(X0) = F’(X0)(X- X0)
Despejamos X
