
viernes, 29 de mayo de 2009
***POLINOMIOS DE NEWTON EN DIFERENCIALES FINITAS***

****METODO DE INTERPOLACION DE NEWTON***
es aproximadamente independiente de x0 y x1 en el rango. Esta razón se conoce con el nombre de primera diferencia dividida de f(x), relativa a x1 y x0, y se designa por medio de f[x1 ,x0]. Se puede inferir de la ecuación que f[x1 ,x0] = f[x0 ,x1]. Por tanto, la linearidad aproximada se puede expresar en la forma f[x0 ,x] f[x1 ,x0] lo que nos lleva a la ecuación de interpolación f(x) f(x0)+ (x -x0).f[x0 ,x1] o la fórmula equilalente.

Quizás Newton genera un método que se le llama "Diferencias Divididas".El origen se emplea de la siguiente forma:

"POLINOMIOS DE LAGRANGE"
 En análisis numérico, el polinomio de Lagrange, llamado así en honor a Joseph-Louis de Lagrange, es el polinomio que interpola un conjunto de puntos dado en la forma de Lagrange.
En análisis numérico, el polinomio de Lagrange, llamado así en honor a Joseph-Louis de Lagrange, es el polinomio que interpola un conjunto de puntos dado en la forma de Lagrange.Dado un conjunto de k + 1 puntos

donde todos los xj se asumen distintos, el polinomio interpolador en la forma de Lagrange es la combinacion lineal
 de bases polinómicas de Lagrange
de bases polinómicas de Lagrange


Se muetra la formula, luego se determina que la viscocidad que alcanza el petroleo a una temperatura de 15 grados centigrados.

"INTERPOLACION"
En esta seccion determinaremos formulas que nos permitan interpolar los valores intermedios entre datos previamente interpolados
*Anlaogico o algebraico
*Polinomios de lagrage
*Diferencias divididas de newton
En unidades posteriores utilizamos estas herramientas para generar metodos que nos permitiran calcular numericamente el valor de integrales,derivadas y que tambien nos permitiran resolver ecuaciones diferenciales de todo tipo.
Empezamos por el Metodo Algebraico:En este metodo esencial se plante a un sistema de ecuasiones aprovechando datos que tenemos:
(Xo,Yo)
(X1,Y1)
(X2.Y2). .. .(Xn,Yn)
lunes, 20 de abril de 2009
actul

Existen muchas formas de resolver estas raices primero estudiaremos como se aplican en el Metodo de Newton-Raphson
Notas sobre el uso de las Raices




Asi mismo los numeros complejos tienen todas las propiedades de los numeros reales
//////////////////////
En este metodo se tiene que despejar a la variable independiente:

donde es la funcion de busqueda que cumple el problema de convergencia.


Ejemplo:
1.- x - cosx = 0
x = cos x ..... 1
cos-1x = x .... 2

///////////////////////
El metodo de la secante
Ecuacion de Newton-Raphson:

la definicion dederivada si escogieramos 2 numeros n+1 y Xn muy cercanos

EN donde Xo es la "peor aproximacion" y Xi es la "aproximacion mejorada"
Xo es la aproximacion tal que:
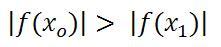
////////
Metodo de Newton-Raphson
martes 24 de marzo de 2009 Publicado por . en 19:21

la recta tangente k se observa que:
dy/dx = m= cte
dy = mdx= F’(X0)(X- X0)
y – y0 = F’(X0)(X- X0)
F(x)- F(X0) = F’(X0)(X- X0)
- F(X0) = F’(X0)(X- X0)
Despejamos X

jueves, 26 de marzo de 2009
**METODO DE LA SECANTE**
1.-El problema con Newton-Raphson es que no todas las personas tienen una buena habilidad para calcular.
2.-En segundo lugar hacer programas que deriven en automatico es muy dificil
3.-El metodo de la secante representa una posible salida de el metodo de Raphson para demostrarlo observe lo siguiente:

De todo este desarrollo nos da la siguiente formula:

martes, 17 de marzo de 2009
METODO DE NEWTON -RAPHSON
METODO DE LA FALSA POSICION
METODO DE BISECCION
* 1ª paso localizas el intervalo que contenga una raíz.
Raíz (a, b)
* 2ª paso Aplíquela formula.


3ª paso En donde se encuentre la raíz verifique.
f(a) f(Xo)
f(b) f(Xo)
***Alguno de ellos es negativo***
4ª paso Establece tu nuevo sub intervalo.
* 5ª paso Comienza de Nuevo.
Se utiliza la siguiente formula:

sábado, 7 de marzo de 2009
TEORIA DE ERROR
Unidad 1
Teoria de errores
1.1 Importancia Metodos Numericos
1.2 Conceptos Basicos Metodos Numericos cifra significativa precision exactitud incertidumbre y sesgo
1.3 Tipos de errores
1.3.1 Definicion de Error error absoluto y relativo
1.3.2 Error por Redondeo
1.3.3 Error por Truncamiento
1.3.4 Error Numerico Total
1.4 Software Computo Numerico
1.5 Metodos Iterativos
Unidad 2
Metodos de solucion de ecuaciones
2.1 Metodos de Intervalo
2.2 Metodo de Biseccion
2.3 Metodo Aproximaciones Sucesivas
2.3.1 Iteracion y Convergencia de Ecuaciones
Condicion de Lipschitz
2.4 Metodos de Interpolacion
2.4.1 Metodo de Newton Raphson
2.4.2 Metodo de la Secante
2.4.3 Metodo de Aitken
2.5 Aplicaciones
Unidad 3
Metodos de solucion de sistemas de ecuaciones
3.1 Metodos Iterativos Jacobi
3.1.2 Metodo Gauss Seidel
3.2 Sistemas de ecuaciones no lineales
3.2.1 Metodo Iterativo Secuencial
3.3 Iteracion Convergencia Sistemasde Ecuaciones
3.3.1 Sistemas de Ecuaciones de Newton
3.3.2 Metodo de Bairstow
3.4 Aplicaciones
Unidad 4
Diferenciacion e integracion numerica
4.1 Diferenciacion Numerica
4.1.1 Formula Diferencia Progresiva y Regresiva
4.1.2 Formula de Tres Puntos
4.1.3 Formula de Cinco Puntos
4.2 Integracion numerica
4.2.1 Metodo del Trapecio
4.2.2 Metodos de Simpson
4.2.3 Integracion de Romberg
4.2.4 Metodo de Cuadratura Gaussiana
4.3 Integracion Multiple
4.4 Aplicaciones
Unidad 5
Solucion de ecuaciones diferenciales
5.1 Metodos de un Paso
5.1.1 Metodo de Euler y Euler mejorado
5.1.2 Metodo de Runge Kutta
5.2 Metodo de Pasos Multiples
5.3 Sistemas Ecuaciones Diferenciales Ordinarias
5.4 Aplicaciones
El dia 4 de marzo aprendi sobre el tema de la "Teoria de Errores ".
Ya que para contruir un edificio,estructura ,puente, etc. se utilizan mediciones la s cuales estan propensasa un error.Tambien las mediciones dependen de los instrumentos que hayan sido utilizados para realizar las mismas, ya que hay algunas de mayor calidad.Este pequeño ejemplo nos ayudo a obtener la formula para el calculo del error. Se dice que un terreno de area cualquiera como el que se ve en la figura.




De todo esto se obtiene la siguiente formula la cual nos permite calcular el error que se comete al realizar las mediciones.

Ejemplo:
Un albañil mide el marco una ventana con un flexometro
 En donde:
En donde:
Xm=3.15
Ym=2.75
A=XY
=3.15(+0.0010) + 2.75(0.0010)
=+/-0.00315+/-0.00275
=+/-0.00590 m------------es el resultado del error
Tambien podemos calcular formulas que nos permitan calcular errores pero usando el concepto matematico diferencial:
 despues vimos el "Error Conceptual".Esto significa que hay veces cables que usamos y vienen especificados con el error en porcentaje y el cual podemos usar la siguiente formula:
despues vimos el "Error Conceptual".Esto significa que hay veces cables que usamos y vienen especificados con el error en porcentaje y el cual podemos usar la siguiente formula:
 Tambien encontramos al siguiente teorema.
Tambien encontramos al siguiente teorema.
Teorema de la compresión:
Esto es que entre mas cercana a numero "n" los términos de la sucesión cada vez estarán mas cerca entre si en los valor absoluto.
Resolución de ecuaciones no lineales: Se llama ecuaciones no lineales a cual quiera en donde la variable no aparezca con argumento de otra función No lineal
se observo tambien el metodo de biseccion: este se basa en las soluciones de una ecuacion representada por la siguiente figura:
En otras palabras hay un cambio de signo al cruzar el eje.





